FairyPrincessSerenity
Empress of Light
I couldn't find anything on this, so I gave myself a whole heap of stress assembling this logic gate.
What it is... Well, that's easy enough to explain. A basic Faulty Gate is based on probability. It either works or it doesn't. How often it works is based on how many light bulbs are lit. The more there are, the more likely it'll work. That wasn't good enough for me, as I needed something that was "yes or other yes" rather than "yes or no" with a single input. Here's an image of the logic gate with and without wires.
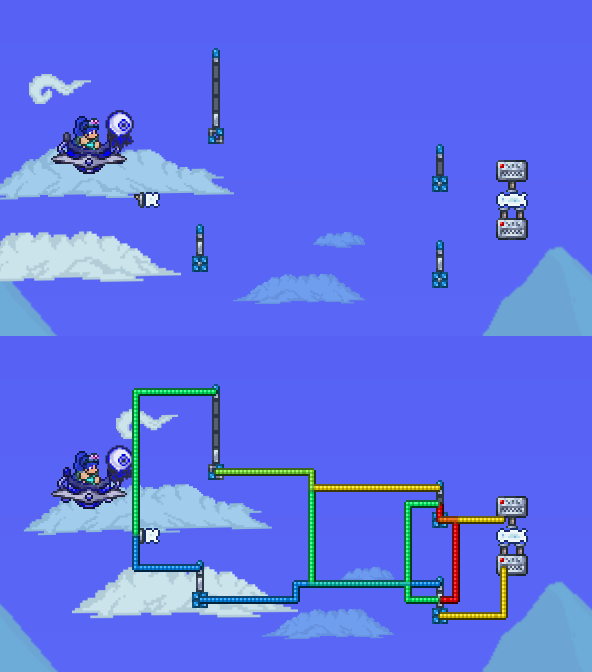
I'll try to explain this mess as best as I can. The input is the switch on the snow block. It activates both halves of the circuit. For reference we'll call the top one Circuit A and the bottom one Circuit B.
Circuit B runs into a Faulty Switch set at 100% probability. This is simply to slow down the current. The blue wire going from that gate connects to the Faulty Bulb on the bottom half of the switch gate. That leads to the yellow wire, which activates the Announcement Board on the bottom. By default the bottom light bulb is always lit.
Circuit A leads into a Faulty Gate that is set to only activate 25% of the time. Attached to that gate are yellow and green wires. The yellow wire connects to the top Faulty Gate while the green wire connects to the light bulbs themselves. This is where it gets technical. The green wires prevent Circuit B from reading the bottom Announcement Board and reads the top Announcement Board instead. The red wire coming out of the top Faulty Gate resets the light bulbs back to the way they were to begin with.
So it's either going to be Circuit A or Circuit B that's going to get activated, never both, but you're always going to get a result.
That's pretty much it. The device can be used for any either/or event that you want. Unmodified, this machine will output a 25%/75% probability of one thing happening versus the other.
-> My gate is specifically based on manipulating the probability between two outcomes. Head on down the thread a bit if it's not what you're looking for. There's a good chance you'll find something useful.
What it is... Well, that's easy enough to explain. A basic Faulty Gate is based on probability. It either works or it doesn't. How often it works is based on how many light bulbs are lit. The more there are, the more likely it'll work. That wasn't good enough for me, as I needed something that was "yes or other yes" rather than "yes or no" with a single input. Here's an image of the logic gate with and without wires.
I'll try to explain this mess as best as I can. The input is the switch on the snow block. It activates both halves of the circuit. For reference we'll call the top one Circuit A and the bottom one Circuit B.
Circuit B runs into a Faulty Switch set at 100% probability. This is simply to slow down the current. The blue wire going from that gate connects to the Faulty Bulb on the bottom half of the switch gate. That leads to the yellow wire, which activates the Announcement Board on the bottom. By default the bottom light bulb is always lit.
Circuit A leads into a Faulty Gate that is set to only activate 25% of the time. Attached to that gate are yellow and green wires. The yellow wire connects to the top Faulty Gate while the green wire connects to the light bulbs themselves. This is where it gets technical. The green wires prevent Circuit B from reading the bottom Announcement Board and reads the top Announcement Board instead. The red wire coming out of the top Faulty Gate resets the light bulbs back to the way they were to begin with.
So it's either going to be Circuit A or Circuit B that's going to get activated, never both, but you're always going to get a result.
That's pretty much it. The device can be used for any either/or event that you want. Unmodified, this machine will output a 25%/75% probability of one thing happening versus the other.
-> My gate is specifically based on manipulating the probability between two outcomes. Head on down the thread a bit if it's not what you're looking for. There's a good chance you'll find something useful.
Last edited:






